
In some cases, there is a possibility to calculate the M.O.I of the circle regarding its axis tangent to the perimeter, then we will practice the parallel axis theorem. Let us just put the value in the integral. Let us just simplify this integration with proper steps:Īs we know about the trigonometric identity i.e. Now, let us just transcribe the integral for the moment of inertia of a circle. Now after the differentiation, the expression will be obtained as Presently, let us just describe the coordinates by applying the polar system.Īfter the completion of step-1, we need to calculate the differential area, which can be achieved by declaring the area of the sector.įrom the image, the area of the sector can be expressed as I y is the component of MOI in the y-axis. Let us just begin by remembering the equation for the second-moment area. This explanation will follow certain steps, such as: The moment of inertia formula of a circle, as per the derivation, the circular cross-section will be calculated with the radius and an axis going exactly through the center.
#Moment of inertia of a circle about its center how to
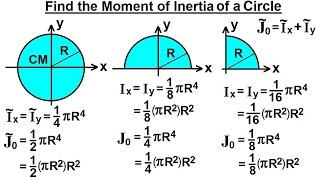
It will be easier to understand how to find moment of inertia of a circle with this derivation. This expression for the moment of inertia of a circle about its diameter can be given asĭo you know how to find the moment of inertia of a circle? To learn about this, we need to understand the derivation of the moment of inertia of a circle, as explained below. If we consider the diameter of a circle D, then we must also take ‘r’ the radius as D/2. Moment of Inertia of a Circle about its Diameter In the case of a quarter circle the expression is given as: In case of a semi-circle the formula is expressed as: In the case of a circle, the polar moment of inertia is given as: Similarly, the moment of inertia of a circle about an axis tangent to the perimeter(circumference) is denoted as: The moment of a circle area or the moment of inertia of a circle is frequently governed by applying the given equation: This equation is equivalent to I D4 / 64 when we express it taking the diameter (D) of the circle. column section to resist buckling is a circular pipe, because it has its area. Moment Of Inertia Of A Circle Here, R is the radius and the axis is passing through the centre. The moment of Inertia formula can be coined as: The Moment of Inertia (I) is a term used to describe the capacity of a. Mathematically, it is the sum of the product of the mass of each particle in the body with the square of its length from the axis of rotation. Yes, the proper definition of the moment of inertia is that a body tends to fight the angular acceleration.

When a body starts to move in rotational motion about a constant axis, every element in the body travels in a loop with linear velocity, which signifies, every particle travels with angular acceleration. It can be inferred that inertia is related to the mass of a body. The moment of inertia of a triangular section of height h, about an axis passing through its center of gravity G and parallel to the base BC, as shown in Fig.
First of all, let us discuss the basic concept of moment of inertia, in simple terms. The moment of inertia of a hollow circular section of outer diameter D and inner diameter d, as shown in Fig.


 0 kommentar(er)
0 kommentar(er)
